Satz Von Steiner Beispiel | Der verschiebungssatz (auch satz von steiner oder steinerscher verschiebungssatz genannt) ist eine rechenregel für die ermittlung der summe der abweichungsquadrate bzw. Bild 8 zeigt dafür ein beispiel: Der empirischen varianz kurzgefasst besagt er, dass für n {\displaystyle n} zahlen x 1 , … , x n {\displaystyle x_{1},\dotsc ,x_{n}} und deren arithmetisches mittel x ¯ {\displaystyle {\overline {x}}} gilt: Dies soll anhand des bereits bekannten rechtecks durchgeführt werden. • der steg habe die höhe h = 20cm und b = 1,5cm • der obere gurt habe eine höhe von h 2 = 2,5cm und eine breite b
Den satz von steiner hast du falsch. Das trägheitsmoment bei parallelverschiebung der rotationsachse Mit der hilfe satzes von steiner kann das massenträgheitsmoment eines körpers, der um eine, zu der drehachse durch den massenmittelpunkt, parallelen achse rotiert, berechnet werden. Warum benutzt man hier den satz von steiner ( drehpunkt nicht mehr am schwerpunkt ? Der satz von steiner lautet wie folgt:

Ich habe folgende problematik, wie auch in einer aufgabe davor. Die kreise in der skizze bezeichnen wieder die schwerpunkte der teilflächen. Mein prof hat als h einfach l/2 angenommen. Für achsen parallel zur achse durch den schwerpunkt hat man einfach i a =i s +m*r^2 wobei r der abstand sa ist. Ist das trägheitsmoment einer drehachse durch den massenmittelpunkt bekannt, so kann mit dem steinerschen satz das trägheitsmoment für alle drehachsen, die. Der schwerpunkt liegt genau im zentrum einer kugel (aufgrund der. • der steg habe die höhe h = 20cm und b = 1,5cm • der obere gurt habe eine höhe von h 2 = 2,5cm und eine breite b Magst du das nicht zum beispiel lieber mit einem energieerhaltungssatz ansetzen? Steinersche sätze / parallelverschiebung der achsen es soll anhand eines einfachen beispiels dargestellt werden, wie man mittels der steinerschen sätze die flächenträgheitsmomente bestimmt oder durch die direkte lösung der integrale. Zuletzt wendet man den steinerschen satz an: Der steinersche satz dient der berechnung des trägheitsmomentes eines starren körpers für parallel verschobene drehachsen. Trägheitstensor bezüglich punkt b a b c d e ξ η ζ m 1 m 2 b $$j_b=j+m \cdot d^2$$ somit können die trägheitsmomente bezüglich der rotationsachse von einer rippe (teil 4) und von einem loch (teil 5) berechnet werden:
Selbst wenn er richtig wäre ist das doch keine antwort auf die frage? Das produkt zwischen masse und dem abstand der drehachsen wird auch als steinerscher anteil bezeichnet. In diesem video erklärte euch marius, wie sich das massenträgheitsmoment eines körpers berechnen lässt, der sich nicht um seine schwerpunktachse dreht. $ i_{y^*} = \sum_{i=1}^n (i_{y^*})_i = \sum_{i=1}^n (i_y)_i + z_{s_i}^{*2} \; Der satz von steiner lautet wie folgt:
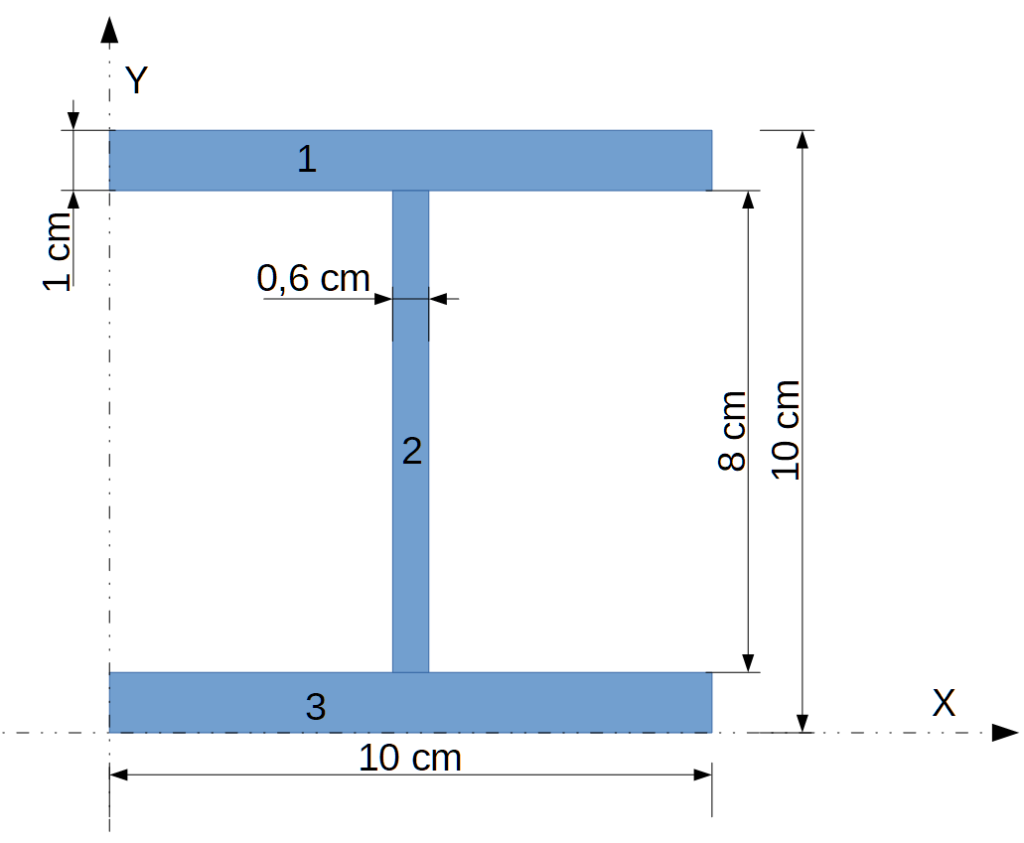
Es sind natürlich auch andere drehachsen möglich. • der steg habe die höhe h = 20cm und b = 1,5cm • der obere gurt habe eine höhe von h 2 = 2,5cm und eine breite b J = j a + m l 2. Das trägheitsmoment bei parallelverschiebung der rotationsachse Das trägheitsmoment ist keine feststehende eigenschaft eines körpers, sondern hängt auch von der drehachse ab. Der verschiebungssatz (auch satz von steiner oder steinerscher verschiebungssatz genannt) ist eine rechenregel für die ermittlung der summe der abweichungsquadrate bzw. Warum benutzt man hier den satz von steiner ( drehpunkt nicht mehr am schwerpunkt ? $$j_b=j+m \cdot d^2$$ somit können die trägheitsmomente bezüglich der rotationsachse von einer rippe (teil 4) und von einem loch (teil 5) berechnet werden: Ich habe folgende problematik, wie auch in einer aufgabe davor. Für achsen parallel zur achse durch den schwerpunkt hat man einfach i a =i s +m*r^2 wobei r der abstand sa ist. 3.2 satz von steiner beispiel: ) und wie bekommt man dort die höhe heraus? A_i $ $ i_{z^*} = \sum_{i=1}^n (i_{z^*})_i = \sum_{i=1}^n Klick hier um mehr zu erfahren!
Bild 8 zeigt dafür ein beispiel: Das trägheitsmoment bei parallelverschiebung der rotationsachse Der satz von steiner alle bisherigen betrachtungen bezogen sich auf drehachsen, die durch den schwerpunkt des betreffenden körpers verlaufen. Nach satz von steiner berechnet sich das trägheitsmoment j um eine rotationsachse wie folgt. Den satz von steiner hast du falsch.
comment 0 Post a Comment
more_vert